This article summarized the famous sorting algorithms, including insertion sort
- Insertion sort - O(N) / O(N^2) [Best case / Worst case]
Insertion sort consists of n - 1 passes. For pass p = 2 through n, insertion sort ensures that the elements in positions 1 through p are in sorted order. Insertion sort makes use of the fact that elements in positions 1 through p - 1 are already known to be in sorted order.
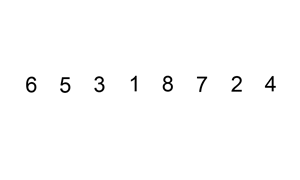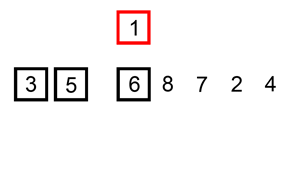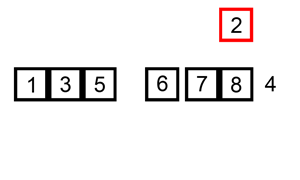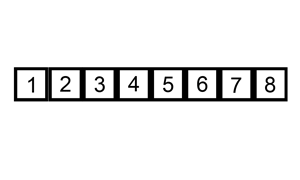
void InsertionSort(ElementType A[], int N)
{
int j, P;
ElementType Temp;
for (P = 1; P < N; P++)
{
Temp = A [P];
for(j = P; j > 0 && A[j-1] > Temp; j--)
{
A[j] = A[j-1];
}
A[j] = Temp;
}
}
- Bubble sort - O(N) / O(N^2)
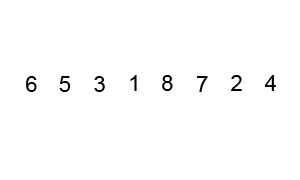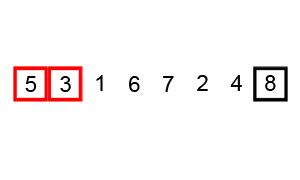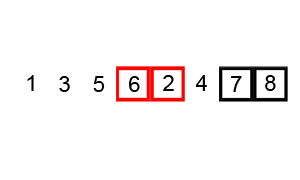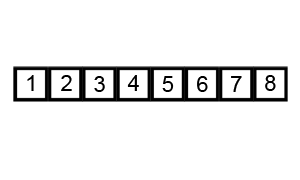
Starting from the beginning of the list, compare every adjacent pair, swap their position if they are not in the right order (the latter one is smaller than the former one). After each iteration, one less element (the last one) is needed to be compared until there are no more elements left to be compared.
void BubbleSort(ElementType A[], int N)
{
int i, j;
ElementType Temp;
for (i = 0; i < N-1; i++)
{
for(j = 0; j < N - 1 - i; j++)
{
if(A[j] > A [j+1])
{
Temp = A[j];
A[j] = A[j+1];
A[j+1] = Temp;
}
}
}
}
- Selection sort - O(N^2)
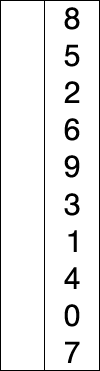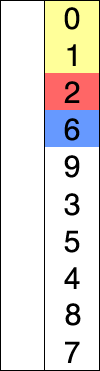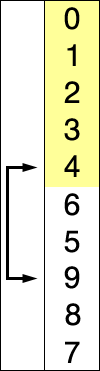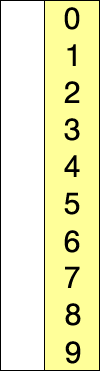
The algorithm divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
void SelectionSort(ElementType A[], int N)
{
int i, j, Min;
ElementType Temp;
for(i = 0; i < N - 1 ; i++)
{
Min = i;
for(j = i + 1; j < N ; j++ )
{
if(A[Min] > A [j])
min = j;
}
Temp = A[Min];
A[Min] = A[i];
A[i] = Temp;
}
}
- Shell sort - O(N^2)
Shell sort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every h-th element gives a sorted list. Such a list is said to be h-sorted.
The first pass, 5-sorting, performs insertion sort on separate subarrays (a1, a6, a11), (a2, a7, a12), (a3, a8), (a4, a9), (a5, a10). For instance, it changes the subarray (a1, a6, a11) from (62, 17, 25) to (17, 25, 62). The next pass, 3-sorting, performs insertion sort on the subarrays (a1, a4, a7, a10), (a2, a5, a8, a11), (a3, a6, a9, a12). The last pass, 1-sorting, is an ordinary insertion sort of the entire array (a1,…, a12).
Shellsort is unstable: it may change the relative order of elements with equal values. It is an adaptive sorting algorithm in that it executes faster when the input is partially sorted.

void ShellSort(ElementType A[], int N)
{
int i,j,Increment;
ElementType Temp;
for(Increment = N/2; Increment > 0; Increment /= 2)
{
for(i = Increment; i < N; i++)
{
Temp = A[i];
for(j = i; j >= Increment; j -= Increment)
{
if(Temp < A[j - Increment])
A[j] = A[j - Increment];
else
break;
}
A[j] = Temp;
}
}
}
- Heap sort - O(NlogN)
The heapsort algorithm involves preparing the list by first turning it into a max heap. The algorithm then repeatedly swaps the first value of the list with the last value, decreasing the range of values considered in the heap operation by one, and sifting the new first value into its position in the heap. This repeats until the range of considered values is one value in length.
#define LeftChild(i) (2 * (i) + 1)
void PerDown(ElementType A[], int i, int N)
{
int Child;
ElementType Temp;
for(Temp = A[i]; LeftChild(i) < N; i = Child)
{
Child = LeftChild(i);
if(Child != N - 1 && A[Child + 1] > A[Child])
Child ++;
if(Temp < A[Child])
A[i] = A[Child];
else
break;
}
A[i] = Temp;
}
void HeapSort(ElementType A[], int N)
{
int i;
for(i = N / 2; i >= 0; i--) /* Build Heap */
PerDown(A, i, N);
for(i = N - 1; i > 0; i--) /* Delete Max */
{
Swap(&A[0], &A[i]);
PerDown(A, 0, i);
}
}
- Quick sort - O(NlogN) / O(N^2)
Quicksort is a divide and conquer algorithm. Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays.
The steps are:
-
Pick an element, called a pivot, from the array.
-
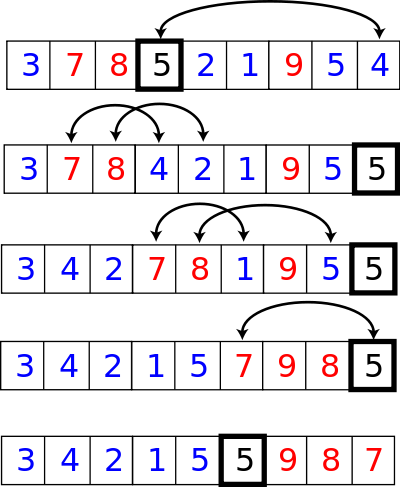
Reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
-
Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
The base case of the recursion is arrays of size zero or one, which never need to be sorted.
void QuickSort(ElementType A[], int N)
{
Qsort(A, 0, N - 1);
}
/* Return median of Left, Center and Right */
/* Order these and hide the pivot */
ElementType Median3(ElementType A[], int Left, int Right)
{
int Center = (Left + Right) / 2;
if(A[Left] > A[Center])
Swap(&A[Left], &A[Center]);
if(A[Left] > A[Right])
Swap(&A[Left], &A[Right]);
if(A[Center] > A[Right])
Swap(&A[Center], &A[Right]);
/* Invariant: A[Left] <= A[Center] <= A[Right] */
Swap(&A[Center], &A[Right - 1]); /* Hide pivot */
return A[Right - 1]; /* Return pivot */
}
#define Cutoff (3)
void QSort(ElementType A[], int Left, int Right)
{
int i, j;
ElementType Pivot;
if(Left + Cutoff <= Right)
{
Pivot = Median3(A, Left, Right);
i = Left; j = Right - 1;
for( ; ; )
{
while(A[++i] < Pivot) {}
while(A[--j] < Pivot) {}
if(i < j)
Swap(&A[i], &A[j]);
else
break;
}
Swap(&A[i], &A[Right - 1]); /* Restroe pivot */
QSort(A, Left, i - 1);
QSort(A, i + 1, Right);
}
else /* Do an insertion sort on the subarray */
InsertionSort(A + Left, Right - Left + 1);
}
P.S. Don’t write code like this, since there is an endless loop if A[i] = A[j] = Pivot.
i = Left + 1; j = Right - 2;
for( ; ; )
{
while(A[i] < Pivot) i++;
while(A[j] < Pivot) j--;
if(i < j)
Swap(&A[i], &A[j]);
else
break;
}
- Merge sort - O(NlogN)
Conceptually, a merge sort works as follows:
-
Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
-
Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.
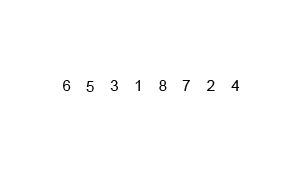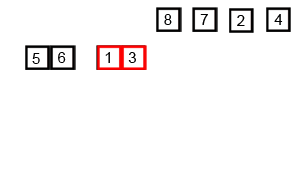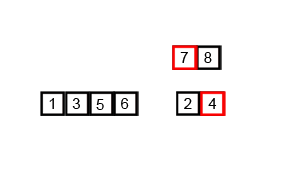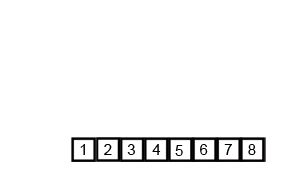
void MSort(ElementType A[], ElementType TmpArray[], int Left, int Right)
{
int Center;
if(Left < Right)
{
Center = (Left + Right) / 2;
MSort(A, TmpArray, Left, Center);
MSort(A, TmpArray, Center + 1; Right);
Merge(A, TmpArray, Left, Center + 1, Right);
}
}
void MergeSort(ElementType A[], int N)
{
ElementType *TmpArray;
TmpArray = malloc(N * sizeof(ElementType));
if(TmpArray != NULL)
{
MSort(A, TmpArray, 0, N - 1);
free(TmpArray);
}
else
FataError("No space for tmp array!!!");
}
/* Lpos = start of left half, Rpos = start of right half */
void Merge(ElementType A[], ElementType TmpArray[], int Lpos, int Rpos, int RightEnd)
{
int i, LeftEnd, NumElements, TmpPos;
LeftEnd = Rpos - 1;
TmpPos = Lpos;
NumElements = RightEnd - Lpos + 1;
/* main loop */
while(Lpos <= LeftEnd && Rpos <= RightEnd)
if(A[Lpos] <= A[Rpos])
TmpArray[TmpPos++] = A[Lpos++];
else
TmpArray[TmpPos++] = A[Rpos++];
while(Lpos <= LeftEnd) /* Copy rest of first half */
TmpArray[TmpPos++] = A[Lpos++];
while(Rpos <= RightEnd) /* Copy rest of second half */
TmpArray[TmpPos++] = A[Rpos++];
/* Copy TmpArray back */
for(i = 0; i < NumElements; i++, RightEnd--)
A[RightEnd] = TmpArray[RightEnd];
}
Updated, Dec. 3rd, 2015.

This work is licensed under a CC A-S 4.0 International License.